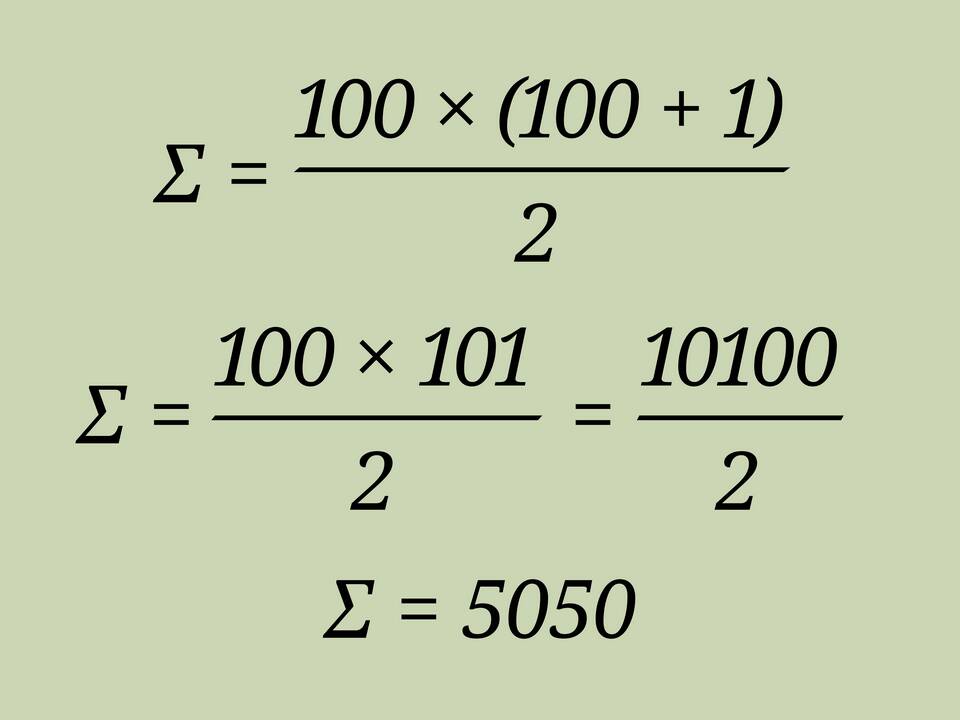Вычисление суммы разностей чисел - это математическая операция, которая часто применяется в статистике, анализе данных и финансовых расчетах. Рассмотрим основные методы и примеры таких вычислений.
Содержание
Основные понятия
| 1. | Разность чисел | Результат вычитания одного числа из другого (a - b) |
| 2. | Сумма разностей | Сложение нескольких разностей между числами |
Способы вычисления суммы разностей
Для двух пар чисел
Формула: (a - b) + (c - d)
- Вычислите первую разность (a - b)
- Вычислите вторую разность (c - d)
- Сложите полученные результаты
Для последовательности чисел
- Создайте пары чисел для сравнения
- Для каждой пары вычислите разность
- Суммируйте все полученные разности
Примеры расчетов
| Пример 1 | (10 - 5) + (8 - 3) = 5 + 5 = 10 |
| Пример 2 | (15 - 10) + (20 - 15) + (25 - 20) = 5 + 5 + 5 = 15 |
| Пример 3 | (7 - 12) + (9 - 5) = (-5) + 4 = -1 |
Практическое применение
- Анализ изменения показателей во времени
- Сравнение данных между группами
- Расчет суммарных отклонений от нормы
- Финансовые расчеты доходов и расходов
Особые случаи
Разности с модулями
Формула: Σ|a - b|
- Вычисляется абсолютное значение каждой разности
- Затем результаты суммируются
Взвешенные разности
- Каждой разности присваивается коэффициент
- Разности умножаются на свои веса
- Произведения суммируются
Проверка правильности вычислений
| 1. | Пересчет в обратном порядке |
| 2. | Использование альтернативных методов |
| 3. | Применение калькулятора |
Полезные советы
- Группируйте положительные и отрицательные разности
- Используйте скобки для четкого обозначения операций
- Проверяйте знаки перед числами
- Для больших массивов данных используйте таблицы
Вычисление суммы разностей чисел - это важный математический навык, который можно освоить, следуя четкому алгоритму. Практика на конкретных примерах поможет лучше понять и запомнить этот метод расчетов.