Сумма углов - это важное геометрическое понятие, которое описывает общую мера углов в конкретной фигуре или при определенных условиях. Это фундаментальное свойство геометрических фигур имеет практическое значение в различных областях математики и ее приложениях.
Содержание
Основные понятия о сумме углов
Сумма углов зависит от типа геометрической фигуры и ее свойств. Рассмотрим основные случаи:
Сумма углов треугольника
Во всех треугольниках на плоскости сумма внутренних углов всегда равна 180 градусам. Это фундаментальное свойство евклидовой геометрии.
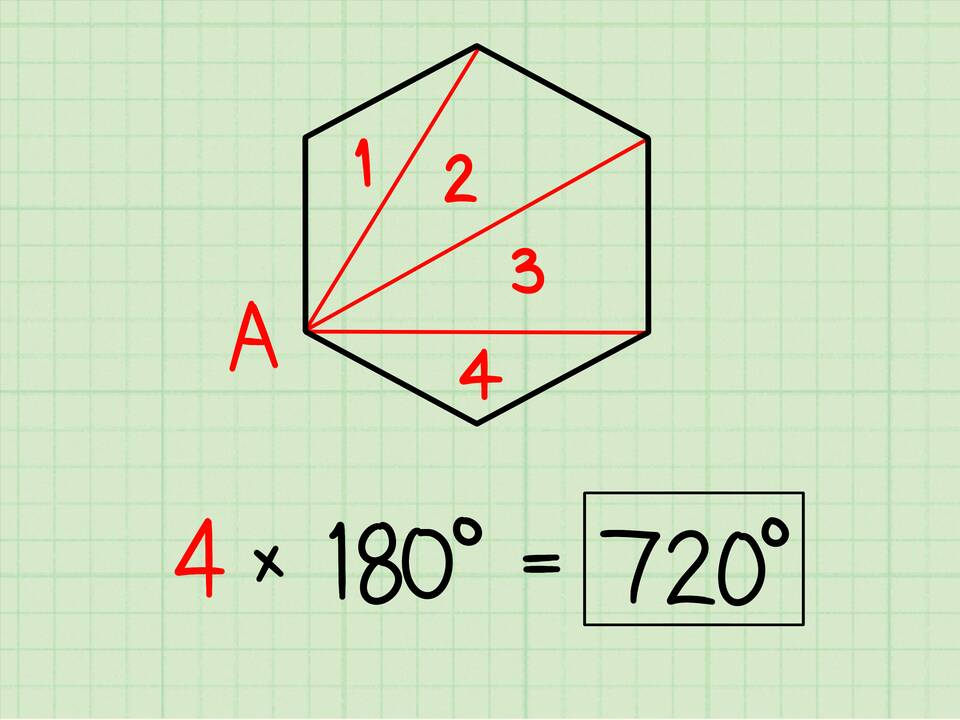
Сумма углов многоугольника
Для выпуклого n-угольника сумма внутренних углов вычисляется по формуле: (n-2) × 180°, где n - количество сторон.
| Фигура | Количество сторон | Сумма углов |
| Треугольник | 3 | 180° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 540° |
Дополнительные случаи
Сумма внешних углов
Для любого выпуклого многоугольника сумма внешних углов (по одному при каждой вершине) всегда равна 360 градусам, независимо от количества сторон.
Углы при пересечении прямых
- Сумма смежных углов равна 180°
- Вертикальные углы равны
- Сумма углов вокруг точки составляет 360°
Практическое применение
Знание суммы углов используется в различных областях:
- Архитектура и строительство
- Геодезия и картография
- Компьютерная графика
- Навигационные системы
- Конструирование механизмов
Особые случаи
Неевклидова геометрия
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а в сферической геометрии - всегда больше 180°.
Звездчатые многоугольники
Для звездчатых многоугольников применяются специальные формулы вычисления суммы углов, учитывающие их сложную структуру.
Заключение
Сумма углов является важной характеристикой геометрических фигур, позволяющей решать множество практических задач. Понимание этого понятия и умение применять соответствующие формулы необходимо для работы в различных технических и научных областях.