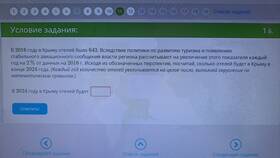
Проценты - одна из самых распространенных математических концепций, применяемая в повседневной жизни, финансах и науке. В этой статье мы разберем основные типы задач на проценты и методы их решения.
Содержание
Основные понятия
| Термин | Определение |
| Процент | Сотая часть числа (1% = 1/100 = 0.01) |
| База | Исходное число, от которого вычисляются проценты |
| Процентная ставка | Величина процентов, выраженная в % |
Основные формулы
Нахождение процента от числа
Формула: (Число × Процент) / 100
Пример: Найти 15% от 200
Решение: (200 × 15) / 100 = 30
Нахождение числа по его проценту
Формула: (Часть × 100) / Процент
Пример: Число 40 составляет 20% от искомого числа
Решение: (40 × 100) / 20 = 200
Нахождение процентного отношения
Формула: (Часть / Целое) × 100%
Пример: Какой процент составляет 25 от 50
Решение: (25 / 50) × 100% = 50%
Типовые задачи и алгоритмы решения
Увеличение на процент
- Находим процент от числа
- Прибавляем полученное значение к исходному числу
Пример: Увеличить 80 на 25%
Решение: 80 + (80 × 25)/100 = 80 + 20 = 100
Уменьшение на процент
- Находим процент от числа
- Вычитаем полученное значение из исходного числа
Пример: Уменьшить 150 на 30%
Решение: 150 - (150 × 30)/100 = 150 - 45 = 105
Последовательное изменение процентов
Формула: Число × (1 ± p₁/100) × (1 ± p₂/100) × ...
Пример: Число 200 увеличили на 10%, затем уменьшили на 5%
Решение: 200 × 1.10 × 0.95 = 209
Сложные проценты
| Параметр | Формула |
| Конечная сумма | S = P × (1 + r/100)n |
| Где: | P - начальная сумма r - процентная ставка n - количество периодов |
Пример: Вклад 1000 руб. под 5% годовых на 3 года
Решение: 1000 × (1 + 5/100)3 ≈ 1157.63 руб.
Практические советы
- Всегда проверяйте, от какого числа берется процент
- Для быстрого счета: 10% = 1/10, 20% = 1/5, 25% = 1/4
- При работе с калькулятором используйте десятичные дроби (5% = 0.05)
- Внимательно читайте условие задачи - важно, что требуется найти
Освоив эти базовые принципы, вы сможете решать большинство практических задач, связанных с процентами.